Think like a butterfly

Introduction

Low-Rank Adaptation (LoRA) is an innovative technique in machine learning, particularly useful for fine-tuning large language models. This post will explore how LoRA adapters work, why they’re efficient, and their practical applications in model adaptation.

What are LoRA Adapters?

LoRA adapters are a method to efficiently fine-tune large neural networks with significantly fewer parameters. The key steps in implementing LoRA are:

1. Freezing the pre-trained model weights
2. Adding small, trainable rank decomposition matrices to each layer
3. Training only these small matrices, reducing memory and computation requirements

The Mathematics Behind LoRA

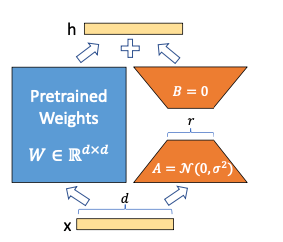
To understand LoRA, we need to delve into some basic matrix computations. In a neural network, each layer typically involves a weight matrix W ∈ ℝ^(d×k), where d and k are the input and output dimensions respectively.

In traditional fine-tuning, you would update the entire weight matrix W. This requires storing and updating d × k parameters.

LoRA, instead, approximates the weight updates using a low-rank decomposition:

ΔW = BA

Where:

• B ∈ ℝ^(d×r)
• A ∈ ℝ^(r×k)
• r is the rank (typically r << min(d,k))

The final weight matrix is then:

W’ = W + ΔW = W + BA

This approach reduces the number of trainable parameters from d × k to r(d + k).

Why is LoRA Efficient?

1. Parameter Efficiency: LoRA reduces the number of trainable parameters from d × k to r(d + k), where r is typically much smaller than d and k.
2. Memory Efficiency: Less memory is required for storing gradients and optimizer states.
3. Computational Efficiency: Fewer parameters lead to faster training and inference times.
4. Adaptability: Multiple LoRA adapters can be trained for different tasks and swapped efficiently without changing the base model.

in more detailed operations

1. Role of gradient descent updates:

Gradient descent updates play a crucial role in training neural networks:

a) They adjust the model parameters to minimize the loss function. b) Each update moves the parameters in the direction that reduces the error. c) Over many iterations, these updates accumulate to transform the initial random weights into meaningful representations.

2. The matrix as a sum of initial values and updates:

The statement “any matrix of model parameters in a neural network of a trained model is just a sum of the initial values and the following gradient descent updates learned on the training data mini-batches” is a key insight behind LoRA. Let’s break it down:

a) Initial state: W₀ (initial random weights) b) After training: W = W₀ + ΔW Where ΔW is the cumulative effect of all gradient descent updates.

3. Why this works in LoRA:

LoRA leverages this insight by approximating ΔW with a low-rank matrix:

W = W₀ + ΔW ≈ W₀ + BA

Where:

• W₀ is the pretrained model’s weights (frozen in LoRA)
• BA is the low-rank approximation of the cumulative updates

4. Simple proof/justification:

Let’s construct a simple proof to illustrate this concept:

Step 1: Initial weights W₀ = initial random weights

Step 2: First gradient descent update W₁ = W₀ + η∇L₁ Where η is the learning rate and ∇L₁ is the gradient of the loss for the first mini-batch.

Step 3: Second update W₂ = W₁ + η∇L₂ = (W₀ + η∇L₁) + η∇L₂ = W₀ + η(∇L₁ + ∇L₂)

Step 4: After n updates Wₙ = W₀ + η(∇L₁ + ∇L₂ + … + ∇Lₙ) = W₀ + ΔW

Where ΔW = η(∇L₁ + ∇L₂ + … + ∇Lₙ) is the cumulative effect of all updates.

Step 5: LoRA approximation LoRA approximates ΔW with a low-rank matrix BA: Wₙ ≈ W₀ + BA

This approximation works because:

1. The cumulative updates ΔW often lie in a low-dimensional subspace of the full parameter space.
2. The most important directions of change can be captured by a low-rank matrix.
3. BA can adapt to approximate the cumulative effect of many small updates.

Mathematical Insight

The efficiency of LoRA stems from the realization that any matrix of model parameters in a neural network can be expressed as:

W_t = W_0 + ΔW

Where W_0 is the initial value and ΔW represents the updates from gradient descent. LoRA approximates ΔW with a low-rank matrix, capturing the most important directions of change in the weight space.

below is the visual representation of it, (excerpt from the original paper)

Practical Implications

1. Resource Optimization: LoRA enables fine-tuning of large models on consumer-grade hardware.
2. Rapid Prototyping: Faster iteration cycles for model adaptation and experimentation.
3. Model Composition: Different LoRA adapters can be combined or interpolated for multi-task learning.

Conclusion

LoRA adapters represent a significant advancement in the field of model fine-tuning. By leveraging low-rank approximations, they offer a mathematically elegant and computationally efficient solution to the challenges of adapting large language models. As the field of AI continues to evolve, techniques like LoRA will play a crucial role in making powerful models more accessible and adaptable to diverse applications.